Order in Chaos

Physicists classify phases of matter as ordered, like crystals, and disordered, like gases, based on the symmetry of this order.

From a philosophical standpoint, matter is a controversial subject, lacking a precise definition.

In economic terms, we view matter as any asset that can be valued in monetary terms (has mass) and occupies a space in current legislation, meaning it is partially or fully recognized by existing, not future, regulations.

The less an asset is defined in legislation, the more disordered it becomes (in terms of quantification), while the more clearly defined it is, the more orderly it becomes.

We can define antimatter as the Solvency Capital Requirement (SCR) or the additional capital required or even provision, calculated using actuarial techniques that are based on the present value of future outcomes.

What matters, then, is not the asset’s progress to date but how it will develop in the future—what mass it will have, with mass measured in the current space, not future, as it will be evaluated based on present legislation.

If the estimated value of the asset is less than that of antimatter, the asset becomes harmful, and risk mitigation is required. Should this asset be recognized—can it be assumed to be under control?

At present, such an asset is recognized in accounting, but additional capital (antimatter) is required to support this harmful asset.

Additionally, we believe harmful assets should be accompanied by a mitigation procedure that generates positive value (matter > antimatter) in order to be recognized and reclassified as non-harmful.

The Trillion Dollar Equation,

$$ {\frac {\partial V}{\partial t}}+{\frac {1}{2}}\sigma ^{2}S^{2}{\frac {\partial ^{2}V}{\partial S^{2}}}=rV-rS{\frac {\partial V}{\partial S}} $$

captures the same principles. The right-hand side is the riskless return from a long position in the present value of derivative $V$ and a short position consisting of ${\textstyle {\partial V}/{\partial S}}$ shares of the underlying asset $S$. The left-hand side consists of a time decay term, leading to increasing entropy.

If that’s not enough, the derivatives market is mulptiles¹ of the underlying securities market on which they are based. This means that we are creating versions of the actual world—virtual worlds that should solve actual problems, market inefficiencies.

Returning to the equation, it remains valid under the assumption of an arbitrage-free market, where no one can outperform the market. Through dynamic hedging, the initial probability of an upward movement should be recalibrated according to the new environment.

When valuing derivatives (options), it is not the actual probabilities p of price changes that matter, but solely the mathematically equivalent probabilities p* under which the option prices exclude all types of arbitrage opportunities a*ccording to the expected value principle.

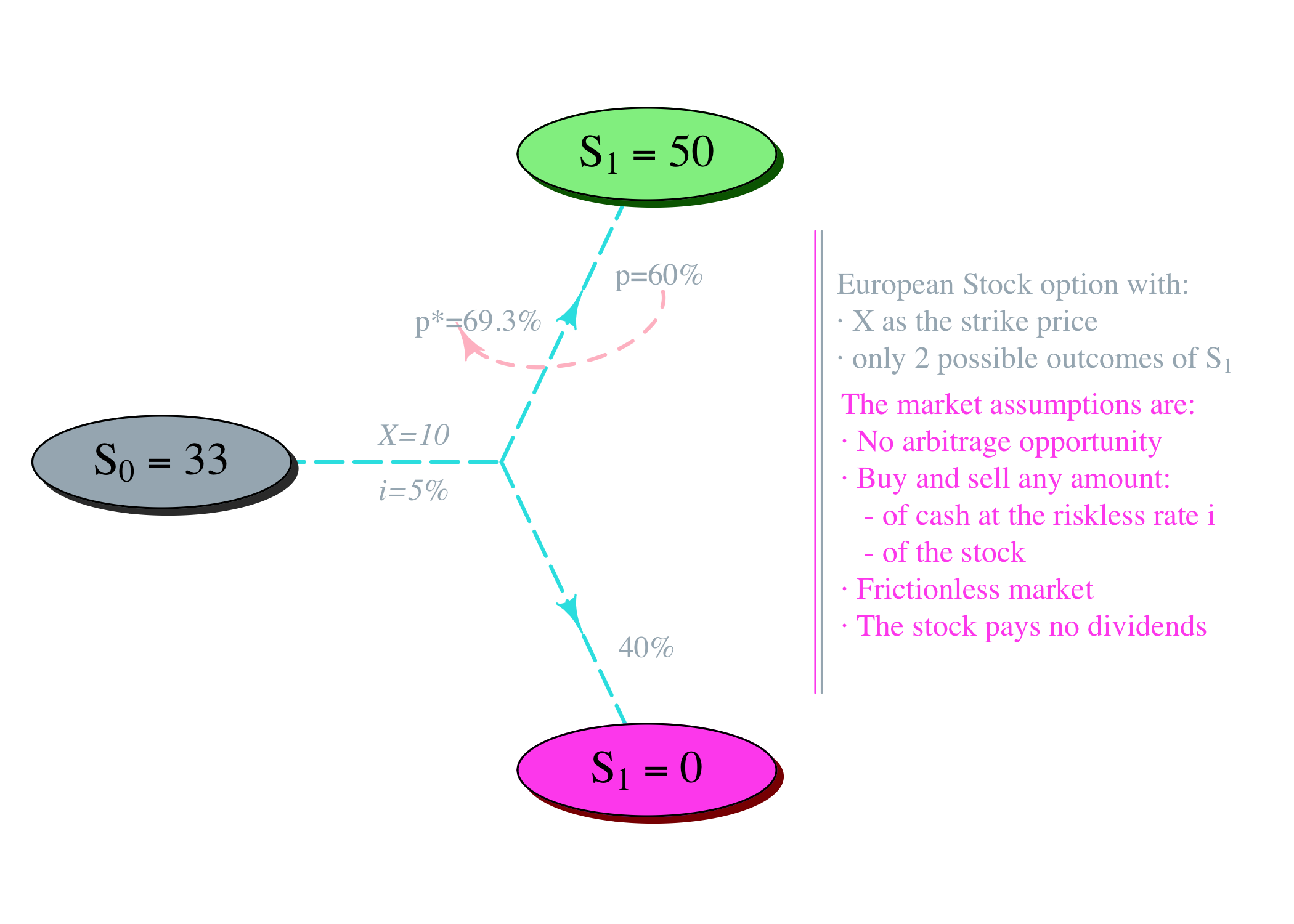
Figure 1: Recalibration of the initial probability after creating versions of the actual world

This approach is characteristic of the entire field of Stochastic or Actuarial Financial Mathematics! No need to understand all of this—just find the best certified actuary who will handle everything for you!