Fizicienii clasifică fazele materiei ca ordonate, precum cristalele, și dezordonate, precum gazele, pe baza simetriei acestei ordini.
Din punct de vedere filozofic, materia este o temă controversată, lipsindu-i o definiție precisă.
În termeni economici, vedem materia ca orice activ care poate fi evaluat în termeni monetari (are masă) și ocupă un spațiu în legislația actuală, adică este recunoscut parțial sau total de normele existente, nu viitoare.
 Cu cât un activ este mai puțin definit în legislație, cu atât devine mai dezordonat (în sensul cuantificării sale), iar cu cât este mai clar definit, cu atât devine mai ordonat.
Cu cât un activ este mai puțin definit în legislație, cu atât devine mai dezordonat (în sensul cuantificării sale), iar cu cât este mai clar definit, cu atât devine mai ordonat.
Putem defini antimateria ca cerința de capital de solvabilitate (SCR) sau capitalul suplimentar necesar, calculat folosind tehnici actuariale bazate pe valoarea prezentă a efectelor viitoare.
Așadar, contează nu progresul activului până în prezent, ci modul în care acesta se va dezvolta în viitor — ce masă va avea, cu masa măsurată în spațiul actual, nu viitor, deoarece va fi evaluată pe baza legislației actuale.
Dacă valoarea estimată a activului este mai mică decât antimateria, activul devine nociv, iar mitigarea riscului este necesară. Ar trebui recunoscut acest activ—poate fi considerat sub control?
În prezent, un astfel de activ este recunoscut contabil, dar este necesar un capital suplimentar (antimateria) pentru a susține acest activ nociv.
În plus, considerăm că activele nocive ar trebui însoțite de o procedură de mitigare care generează o valoare pozitivă (materie > antimaterie) pentru a fi recunoscute și declasificate ca fiind non-nocive.
Ecuația de trilioane de dolari,
$$ {\frac {\partial V}{\partial t}}+{\frac {1}{2}}\sigma ^{2}S^{2}{\frac {\partial ^{2}V}{\partial S^{2}}}=rV-rS{\frac {\partial V}{\partial S}} $$
pune în lumină aceleași principii. Partea dreaptă a ecuației reprezintă rentabilitatea fără risc dintr-o poziție lungă a valorii prezente a derivatului $V$ și o poziție scurtă constând din ${\partial V}/{\partial S}$ acțiuni ale activului de bază $S$. Partea stângă propune termenul de dezintegrări în timp, ceea ce conduce la creșterea entropiei.
Dacă acest lucru nu este suficient, piața derivatelor este scalată1 față de piața de instrumente de bază pe care se construiesc. Aceasta înseamnă să creăm versiuni ale lumii reale—unele virtuale care ar trebui să rezolve problemele reale, corectând ineficiențele din piață.
Revenind la ecuație, aceasta rămâne valabilă sub presupunerea unei piețe fără arbitraj, unde nimeni nu poate depăși piața. Prin hedging dinamic, probabilitatea inițială a unei mișcări ascendente ar trebui recalibrată conform noului mediu.
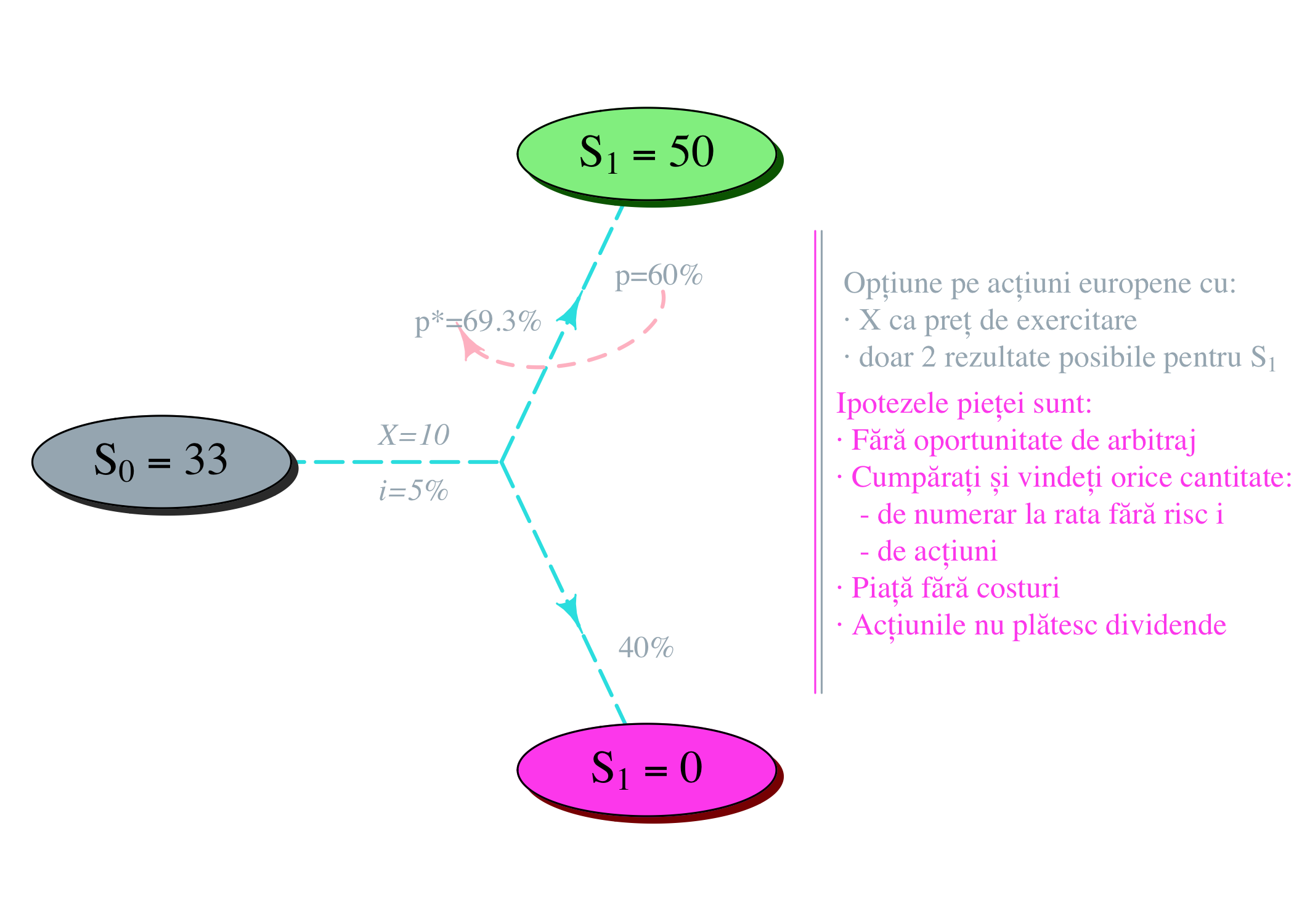
Figura 1: Recalibrarea probabilității inițiale după crearea noilor versiuni adaptate la lumea reală
 Nu trebuie să înțelegi toate acestea doar găsește cel mai bun actuar certificat care să construiască modelul adecvat!
Nu trebuie să înțelegi toate acestea doar găsește cel mai bun actuar certificat care să construiască modelul adecvat!